6 x 12 8 x 18 4 atomsunit cell Coordination number 12 Close packed directions are face diagonals. 100 1 pt Natoms1.
Linear density is the ratio of the number of atoms present in the direction of the.
Linear density fcc 100. A Derive linear density expressions for FCC 100 and 111 directions in terms of the atomic radius R. B Compute and compare linear density values for these same two directions for copper Cu. Determine the linear density atomsnm for BCC 100 110 and 111 directions in terms of atomic radius R.
100 1 pt Natoms1. LDNatomslength 3 4r Sqrt34r 0433013 r 110 1 pt Natoms1. LDNatomslength 3 2 4r.
1 a Derive linear density expressions for FCC eq100 eq and eq111 eq directions in terms of the atomic radius R. B Compute and compare linear density values for these same two. A Derive linear density expressions for FCC100 and 111 directions in terms of the atomic radius R and b compute linear density values for these two directions for silver.
I atomR b 100. Keeping this in view how is FCC planar density calculated. Find the area of the plane.
As an example the area of a 1 1 0 plane of an FCC crystal is 8_sqrt2_R2 where R is the radius of an atom within the plane. Calculate planar density with the formula. PD Number of atoms centered on a given plane Area of the plane.
Area of the square. 2R2 2. So plannar density of 100 plane.
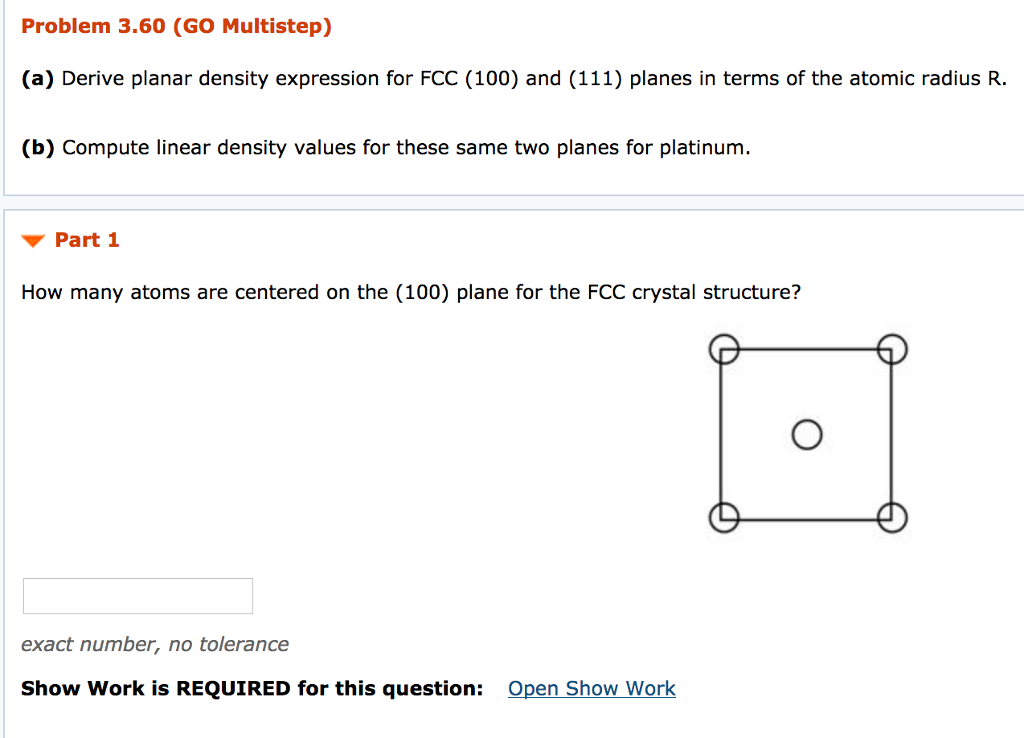
PD 100plane number of atoms centerd at 100 plane area of plane 2 8R2. 1 4R2. There are 6 atoms whose centre lie on this plane.
Total equivalence is 2 atoms associated with this FCC 111 plane at centered. Face-Centered Cubic FCC Structure Unit cell contains. 6 x 12 8 x 18 4 atomsunit cell Coordination number 12 Close packed directions are face diagonals.
LD 110 2 atom4R 12R LD 001 1 atom2R2 12R 2 LD 111 1 atoms4R 12R 6. Draw the atoms on the direction and use the formula. Derive the linear density of 110 100 and 111 of BCC crystal internal of lattice constant.
Linear density is the ratio of the number of atoms present in the direction of the. Materials Science problem deriving the planar density of a Face Centered Cubic unit cell in the 100 and 110 planes. Sample calculations are performed for.
This Is the Most Planar Density in the FCC structure. D 0555 for 110 and d 0785 for 100 𝐴𝑒𝑟𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑃𝑙𝑎𝑛𝑒 111 𝑆 height width. Associated with this FCC 100 plane.
The planar section represented in the above figure is a square wherein the side lengths are equal to the unit cell edge length 2R2 Equation 31. And thus the area of this square is just 2R22 8R2. Hence the planar density for this 100 plane is just PD100 number of atoms centered on 100 plane area of 100 plane.
The Planar Density for FCC 100 plane formula is defined as number of atoms per unit area that are centered on a particular crystallographic plane and is represented as PD 025R 2 or planar_density 025Radius of Constituent Particle 2. The Radius of Constituent Particle is the radius of the atom present in the unit cell. A Derive linear density expressions for FCC 100 and 111 directions in terms of the atomic radius R.
B Compute and compare linear density values for these same two directions for silver. The atomic radius for silver is 0144 nm. A Derive planar density expressions for FCC 100 and 111 planes in terms of the atomic radius R.
A Derive linear density expressions for FCC 100 and 111 directions in terms of the atomic radius R. A Derive linear density expressions for FCC 100 and 111 directions in terms of the atomic radius R. B Compute and compare linear density values for these same two directions for silver.
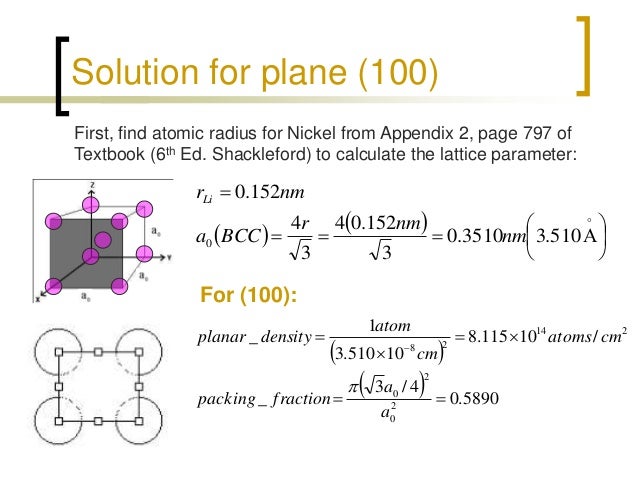
ArialMS PゴシックTimes New RomanSymbolArial Rounded MT BoldChapter_03_aviBitmap ImageLinear and Planar Atomic Densities FCC. Linear DensityP 353 a. Linear Density for BCCPlanar Density of 100 IronP 355 a.
Planar Density for BCCPlanar Density of BCC 111 IronP 354 a. An FCC unit cell within which is drawn a 111 direction is shown below. Thcrc arc six atoms whose ccntcrs lie on this plane Which arc through F.
Onc-sixth of of atoms A D and F arc associated with this planc yielding an equivalence of one-half atom with one-half of cach of atoms. What is the planer density of 100 plane in FCC face-centred cubic crystal with unit cell side a equa. 9 Derive linear density expressions for FCC 100 and 111 directions in terms of the atomic radius R.
10 What are the indices for the two planes drawn in the following sketch. 10 Determine the Miller indices for the planes shown in the following unit cell. For example let us determine the linear density of the 110 direction for the FCC crystal structure.
It is necessary to take into account the sharing of atoms with adjacent unit cells 𝐿𝐷 number of atoms centered on direction vector length of direction vector 𝐿𝐷110 1 2 atom satom1 2 atom 𝑅𝑅𝑅𝑅 𝐿𝐷110. Civil Engineering questions and answers. 1 Derive the linear density for the 100 direction of the FCC unit cell and the 111 direction of the BBB unit cell w 2 Sketch the.
A reduced sphere b atomic packing of an FCC 110 plane. Linear Density of Atoms LD Unit length of direction vector Number of atoms Planar Density atoms Area2D repeat unit Chapter 3 - 14 Planar Density of 100 Iron Solution. At T 912C iron has the BCC structure.
Linear density is the measure of a quantity of any characteristic value per unit of length. Linear mass density and linear charge density are two common examples used in science and engineering. The term linear density is most often used when describing the characteristics of one-dimensional objects although linear density can also be used to describe the density of a three-dimensional quantity along.